Kultainen leikkaus matematiikan ja kuvataiteen työkaluina

 

Kultainen leikkaus matematiikan ja kuvataiteen työkaluina

 

Ilkka Virtanen

 

 

Akropolis-kukkulalla Ateenassa sijaitsevan Pantheonin temppelin arkkitehtuuri perustuu kultaiseen leikkaukseen. Sen pääty noudattaa kultaisen nelikulmion mittasuhteita (Kuva:Wikipedia)

 

 

Maria Wiikin pastellityön ”Vanha nainen sairasvuoteellaan” tulkitaan olevan asettelultaan kultaisen leikkauksen mukainen (Kuva: Gösta Serlachiuksen taidesäätiö, Tomi Aho)

 

Elämme olympialaisten aikaa. Niiden alkujuuret löytyvät antiikin Kreikasta Peloponnesoksen niemimaalla sijainneesta Olympian lehdosta, Zeus-jumalan vanhasta kulttipaikasta. Urheilukulttuurin lisäksi antiikin Kreikassa kukoistivat myös tieteet ja taiteet. Kirjoitukseni aiheena on tuolloin syntynyt geometrinen käsite kultainen leikkaus, jolla on moninaisia sovelluksia matematiikassa ja käyttöalueita eri taiteissa, erityisesti kuvataiteessa, arkkitehtuurissa ja musiikissa. Matematiikka on ominta työaikaista aluettani, kuvataiteet taas tämän blogin luojan ja ylläpitäjän, hyvän ystäväni ja yhteistyökumppanini Aimo Nybergin. Olen kiitollinen Aimolle hänen antamistaan mahdollisuuksista hyödyntää tätä suosittua blogisivustoa kirjallisiin harrastuksiini.

 

Kultainen leikkaus ja kultainen nelikulmio

Kultaista leikkausta tutkivat ensimmäisenä antiikin Kreikan matemaatikot – erityisesti Pythagoras ja Eukleides koulukuntineen - huomattuaan, että suhde esiintyy useissa geometrisissa kuvioissa. Sen tärkeä rooli paitsi matematiikassa myös estetiikassa, arkkitehtuurissa, taiteessa, luonnossa ja musiikissa tunnettiin myös jo tuolloin. Se mitä ihmissilmä näkee, koetaan yleensä esteettisesti kauniiksi ja miellyttäväksi, mikäli näkymä noudattaa kultaisen leikkauksen mittasuhteita.

Kultainen leikkaus eli kultainen suhde saadaan, kun jana (tietyn mittainen suora viiva) jaetaan kahteen osaan niin, että lyhyemmän osan suhde pidempään osaan on sama kuin pidemmän osan suhde koko janaan. Määritystapa on yksi tapa laskea lukujen keskimääräinen arvo (keskiverto) monien muiden keskilukujen (keskiarvo, mediaani, moodi) rinnalla. Pidempi osa on lyhyemmän osan ja koko janan keskiverto.

Kultaisen leikkauksen jakosuhde voidaan määrittää monella tavalla, laskemalla aritmeettisesti tai geometrisesti harpilla ja viivoittimella. Omana kouluaikanani geometrian opetuksessa oli tärkeätä, että geometrisia ongelmia ratkottiin mahdollisimman paljon vain harppia ja viivoitinta hyväksi käyttäen. Tämä opetustapa lienee nyt merkittävästi vähentynyt tai jäänyt kokonaan pois.

Aritmeettisesti ongelma ratkeaa yhtälöä hyväksi käyttäen. Olkoon janan pituus yksikön mittainen (=1), ja merkitään janan pidemmän osan pituutta x:llä. Lyhyemmän osan pituus on tällöin 1-x. Kultaisen leikkauksen määritelmä edellyttää, että voimassa on verranto

(1-x) : x = x : 1 eli perusmuotoiseksi yhtälöksi muokattuna: x² + x - 1 = 0.

Yhtälön (positiivinen) ratkaisu onx = 1 2 ( 5 − 1 )

Pidemmän osan x:n arvo on irrationaalinen päättymätön desimaaliluku, jonka kolmidesimaalinen likiarvo on 0,618. Lyhyempi osa on tällöin 0,382. Osien suhde on suhteellisen lähellä suhdetta 6 : 4 eli 3 : 2, jota kerrotaan käytettävän, kun kultaista leikkausta sovelletaan esim. kuvataiteessa.

Eukleideen tapaa määrittää kultainen leikkaus geometrisesti harpin ja viivoittimen avulla havainnollistaa seuraava kuvio. Jaettavaa janaa on merkitty päätepistekirjaimin A ja B. Janan päätepisteeseen B piirretään kohtisuoraan janaa vastaan janan AB puolikkaan mittainen jana BC. Yhdistetään pisteet A ja C janalla, jolloin saadaan suorakulmainen kolmio ABC. Seuraavaksi piirretään piste C keskipisteenä ja jana CB säteenä ympyränkaari, joka leikkaa janan AC pisteessä D. Lopuksi piirretään piste A keskipisteenä ja jana AD säteenä ympyränkaari, joka leikkaa janan AB pisteessä S. S jakaa janan AB kultaisen leikkauksen mukaisessa suhteessa. Tuloksen todistus sivuutetaan tässä yhteydessä. 

 

 

Kultainen nelikulmio on nelikulmio. jonka sivut suhtautuvat toisiinsa kultaisen leikkauksen mukaisesti. Alkukuvassa olevan Akropolis-kukkulan Pantheon temppelin pääty täyttää hyvinkin tarkasti lappeellaan olevan kultaisen nelikulmion mukaiset suhteet.

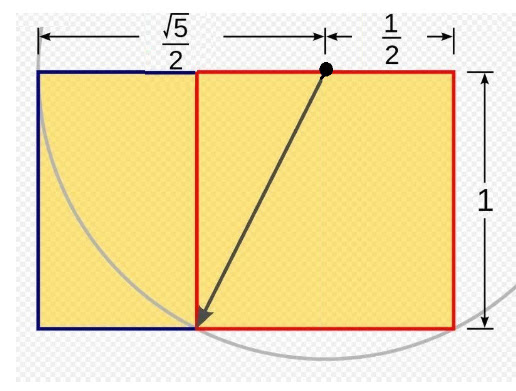
Kultainen nelikulmio voidaan määrittää geometrisesti harpilla ja viivoittimella kun toinen sivuista on kiinnitetty. Tunnetaan esimerkiksi maalauksen leveys lyhyempänä sivuna. Suuriko tulisi olla taulun korkeus? Seuraava kuva havainnollistaa nelikulmion konstruointia.

 

Lähdetään liikkeelle tunnetusta lyhyemmästä sivusta. Valitaan sen pituus mittayksiköksi (= 1). Piirretään (punaisella merkitty) neliö, jonka sivut ovat tuon tunnetun sivun mittaiset. Puolitetaan neliön yläsivu. Yhdistetään yläsivun keskipiste vastakkaisen alasivun kärkipisteeseen (musta nuoli). Piirretään neliön yläsivun keskipiste keskipisteenä ympyränkaari, jonka säde on äsken konstruoitu jana, ympyrä kulkee neliön alasivun kärkipisteiden kautta. Jatketaan yläsivua, kunnes se leikkaa ympyränkaaren. Näin on saatu konstruoiduksi kultaisen nelikulmion pidempi sivu. Täydennetään kuvio suorakulmioksi, kultaiseksi nelikulmioksi. Kuvaan merkityt mitat voidaan helposti määrittää tunnetun Pythagoraan suorakulmaista kolmiota koskevan teoreeman avulla.

Kuvataiteessa käytetään kultaista leikkausta ja kultaista nelikulmiota suunnitteluun ns. kolmanneksen säännön muodossa. Kuva-ala jaetaan pysty- ja vaakasuunnassa kolmanneksiin pysty- ja vaakasuorilla viivoilla. Kolmeen osaan jakaminen perustuu kultaisen säännön käytännön likiarvona käytettyyn sivujen suhteeseen 3 : 2. Olen täysi maallikko kuvataiteen suunnittelu- ym. asioiden suhteen, mutta lyhyellä tutustumisella aihepiiriin olen havainnut kaksi eri lähestymistapaa ruudukon hyödyntämiseksi.

Ensimmäisessä lähestymistavassa viivojen neljän risteyskohdan katsotaan muodostavan kuvan sommittelun kannalta otollisimmat kohteet. Suosimalla sommittelussa näitä kohtia voidaan kuvaan saada enemmän jännitettä, voimaa ja mielenkiintoa kuin esimerkiksi keskeisen kohteen asettamisella keskelle kuvaa. Toisessa tavassa tärkeimmät aiheet sijoitetaan vaaka- tai pystysuunnassa kolmansiin (reuna)ruutuihin.

Palataan vielä alussa esillä olleeseen Maria Wiikin pastellityöhön kolmanneksen säännön toimivuuden testaamiseksi.

 

 

Teoksessa ovat keskeisellä sijalla ilmeisestikin potilaan kasvot ja ristissä olevat kädet. Säännön ensimmäisen lähestymistavan mukaisesti kasvot (pääkohde?) on sijoitettu erinomaisesti ruudukkoviivojen leikkauspisteeseen. Kädet eivät niinkään. Toisella lähestymistavalla on ehkä parempi osuvuus. Kasvot ovat kohtalaisen hyvin vaakasuunnassa vasemmanpuolimaisimmassa kolmanneksessa ja kädet melko hyvin pystysuorassa alimmassa kolmanneksessa ja vaakasuorassa jaossa täysin oikeanpuolimaisimmassa.

 

Kultainen leikkaus muualla matematiikassa

Kultaisen leikkauksen yleisyys arkkitehtuurissa ja kuvataiteissa perustuu siihen, että ihmissilmän näkemä koetaan yleensä esteettisesti kauniiksi ja miellyttäväksi, kun näkymä noudattaa kultaisen leikkauksen mittasuhteita. Kultaisen leikkauksen esiintymisissä matematiikassa toistuu tähän verrattava ominaisuus. Kyseessä on melkein poikkeuksetta matemaattinen elementti tai ongelma, johon liittyy säännöllisyyttä, symmetrisyyttä tai muita vastaavia ominaisuuksia. Seuraavassa on muutama esimerkki tällaisista tapauksista.

Kuvassa on uloimpana säännöllinen kymmenkulmio. Kymmenkulmion ympärille voidaan piirtää ympyrä (keskipiste kymmenkulmion keskipisteessä, ympyrän kaari kulkee kymmenkulmion kärkipisteiden kautta), kuvioon on piirretty kaksi ympyrän sädettä (keltaiset). Ympyrän säteen ja kymmenkulmion sivun suhde on kultainen leikkaus. Kuvioon piirretyt kaksi (keltaista) sädettä ja kymmenkulmion sivu muodostavat tasakylkisen kolmion, jota kutsutaan kultaiseksi kolmioksi. Kolmion kylki ja kanta muodostavat kultaisen leikkauksen. Kolmion huippukulman suuruus (36^o) on puolet kummastakin kantakulmasta (72^o).

Kymmenkulmion sisään on piirretty (punaisella) säännöllinen viisikulmio ja sille (vihreällä) lävistäjät. Lävistäjät ja viisikulmion sivut ovat jälleen kultaisen leikkauksen mukaisessa suhteessa. Lävistäjät jakavat toisensa kolmeen osaan. Jaetun lävistäjän keskiosa on lyhyempi kuin keskenään yhtä pitkät reunaosat. Reunaosa ja keskiosa muodostavat kultaisen leikkauksen.

 

Säännöllisen viisikulmion lävistäjät muodostavat viisisakaraisen tähtikuvion, jota kutsutaan pentagrammiksi. Pentagrammiin liittyvän kultainen leikkaus -ominaisuuden johdosta Pythagoraan kerrotaan valinneen pentagrammin salaseuransa symboliksi. Kuviosta havaitaan, että pentagrammin sisään muodostuu uusi, pienikokoisempi säännöllinen viisikulmio. Tälle voitaisiin edelleen lävistäjien avulla muodostaa uusi pentagrammi, jonka sisään muodostuisi taas uusi viisikulmio. Prosessia voitaisiin jatkaa yhä pienenevin kuvioin rajattomasti. Syntyisi viisikulmioiden (ja pentagrammien) joukko, joka on itsesimilaarinen eli joukko näyttää samalta tai samankaltaiselta, katsoi sitä millä suurennoksella tahansa. Lähestytään fraktaalien maailmaa, joka hämmästyttävän upeine kuvineen (mm. Mandelbrotin joukot) on viime vuosikymmeninä noussut näkyvästi esiin tietokonegrafiikan ja kaaosteorian sovellusten myötä. Ehkä näihin voidaan palata joskus myöhemmin.

Matemaattisten elementtien tietynlaisesta universaalisuudesta kertoo se, että kultainen leikkaus tulee esiin matematiikan myös alueella, jolla ei ole mitään tekemistä ominaisuuden perusalueen, geometrian, kanssa. Aritmetiikassa Fibonaccin luvuilla tarkoitetaan lukujonoa, jonka kaksi ensimmäistä jäsentä ovat 1 ja 1. Seuraavat määräytyvät niin, että jonon jäsen on aina kahden edellisen summa. Saadaan siis lukujono 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …. Kun lasketaan jonon kahden peräkkäisen jäsenen suhde, saadaan jono 1, 2, 1,5, 1,667, 1,6, 1,625, 1,615, 1,619, 1,618, 1,618, … Suhdejonon arvot vuorotellen pienenevät ja kasvavat ja lähestyvät selvästi jotakin tasapainotilaa. Jonon kymmenennen jäsenen kohdalla on jo saavutettu tasapainotila kolmen desimaalin tarkkuudella. Mikä on tämä arvo 1,618? Se on kultaisen leikkauksen pidemmän osan ja lyhyemmän osan suhteen kolmidesimaalinen likiarvo. Fibonaccin luvut kasvavat noudattaen kultaisen leikkauksen lakia! Kultainen leikkaus voitaisiin siten määritellä myös Fibonaccin lukujonosta muodostetun kahden peräkkäisen jäsenen suhdelukujonon raja-arvona, kun jonon pituus lähenee ääretöntä. Matematiikka on täynnä ihmeellisyyksiä.

 

...

 

 Kiitos Ilkka tästä!

 

Aivan erinomainen uuden aihepiirin "sisäänajo" tähän blogiin!

Matematiikkaa on kaikkialla, ymmärrämme sitä tai emme.

 Matematiikka on myös avain kauneuden kokemiseen.

 

Tämä blogi on sitoutumaton ja vapaa julkaisualusta myös 

Sinun kirjoituksillesi ja kuvillesi! 

Sivuston yllätito:

aimonyberg(at)gmail.com